
|
The half-life of an isotope is the time taken for exactly half of the isotope to transform, by radioactive decay, into another element. This is exponential decay. In one half-life interval, half of the original isotope has transformed itself into an isotope of another element. For each individual atom, this is a purely random event, with a particular probability of occurrence. After an interval of ten half-lives, there will be just 1/1024th of that isotope left. Some isotopes, like tellurium-130 which decays by double beta decay, have a half life of 2.4×1021 years, longer than the present age of the Universe at 13.4×1010 yrs, whilst others have half-lives measured in fractions of a second.
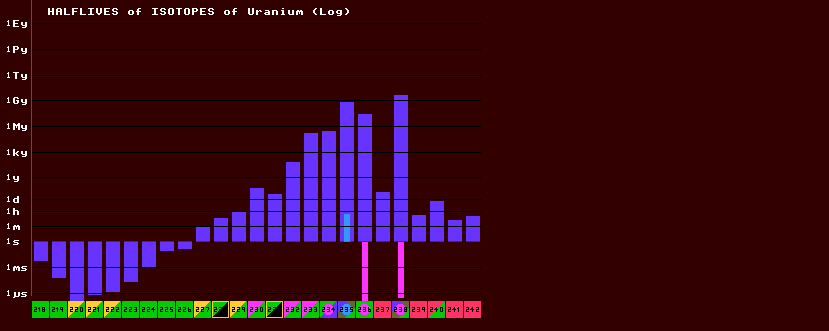
The halflives of metastable nuclides are shown as solid cyan coloured histogram bars for metastable states that decay by other than internal transition (e.g. beta or inverse beta decay), and those for internal transition isomers as hollow cyan bars. Thus in the above halflives of Uranium example, the isotope with the longest halflife is U-238, whilst the shortest halflive is possessed by that of U-220. U-235 has a metastable state, with a shorter halflife (shown in cyan) that the ground state (shown in blue). There are two isotopes with fertile metastable states, with halflives (much shorter that 1 microsecond) shown in magenta. Carbon-14, with a half-life of 5730 years, is useful in radiocarbon dating once living organisms, as, once dead, the ratio of stable 12C to radioactive 14C changes exponentially with time. Several other longer lived isotope pairs are useful in dating rocks and minerals, ground water and polar ice-cores, like 16O/18O, 87Rb/86Sr and 87Sr/86Sr ratios. See RadioMetric Dating.
Abbreviations used are:
|
![]()