SECULAR EQUILIBRIUM


Two nuclides are said to be in secular equilibrium when the daughter nucleus of the parent nuclide is also radioactive, but has a half-life very much shorter than the parent nuclide. Thus the amount of the daughter nuclide remains roughly constant, it is being created almost as fast as it is destroyed, but only so long as the elapsed time is short in comparison to the half-life of the parent nuclide, otherwise the reduction in the amount of the parent results in a reduction in the amount of the daughter. The sun is in a kind of secular equilibrium, looking equally bright from one day to the next, but over aeons, is slowly changing as it consumes its' nuclear fuel. So it is not really in true equilibrium at all, but a quasi-equilibrium, one dependant slightly upon time, a secular equilibrium.

Isotopes in secular equilibrium are in semi-equilibrium. The equilibrium is long term but not permanent because of the slow decay of the source nuclide, hence the term 'secular' meaning slow. Thus, nuclides with geologically short half-lives may exist on Earth by this means. Examples are Radon-222 with a half-life of only 4 days which is being continually created by the radioactive decay of Radium-226 (with a half-life of 1600 years) which is itself created in the radioactive decay series of Uranium-238, which has the very long half-life of 4500 Million years having existed on Earth since Earths' creation.

When two isotopes are in secular equilibrium, it is clear that for every atom of the parent that decays, there is one atom of the daughter that also decays, otherwise the daughter isotope would accumulate. This doubles the apparent activity of the parent.

In natural uranium, which contains U-235 and U-238 and which has existed on Earth for at least 4500 million years, all the daughter isotopes in the decay chains have shorter half-lives than this, so all the daughters are in secular equilibrium, totalling some 35 extra nuclides. For every atom of U-235 and U-238 that decay, 35 other isotopes also decay, increasing the activity well over and above that of either pure U-235 or pure U-238 alone.

When in secular equilibrium, the number of atoms of each intermediate member of a decay series is inversely proportional to its respective decay constant.

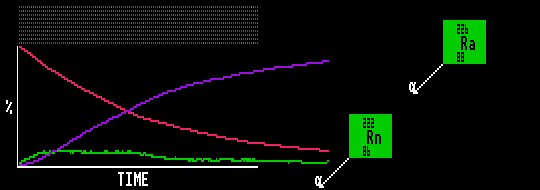
In the animation, the red substance decays into an unstable green substance, which has a halflife 6 times shorter than the red substance. The green substance then quickly decays into a stable blue substance. The quantity of red substance decreases exponentially with time, whilst that of the blue increases. However, the quantity of green substance quickly reaches a quasi-equilibrium when it then remains in direct proportion (1:6) to the slowly decaying red substance.

Shown is Radium-226 slowly decaying into Radon-222 which rapidly disintegrates, but is continually replenished by the decay of Radium-226.