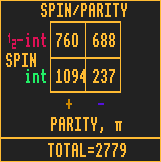


PARITY
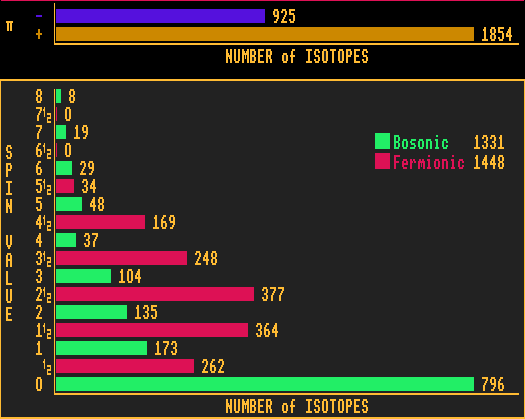
The parity of an isotope can be either even (+) (fawn coloured bar) or odd (-) (blue coloured bar). There are more than twice as many isotopes with even parity than there are with odd parity. Quite what the significance this has, I haven't a clue!
Parity is conserved except in weak interactions (e.g. beta decay processes)
SPIN
By definition, all bosons have integer spin (green coloured bars). Similarly, all fermions have half-integer spin (red coloured bars). Taking all the known isotopes together, there are nearly the same numbers of bosons as fermions.
BOSONIC
All isotopes with zero spin (spin-0) have an even number of protons and an even number of neutrons (even-N, even-Z), thus are composed of a whole number of helium-4 nuclei. As can be seen, most bosons have zero spin, and the higher the spin, the fewer bosonic isotopes.
FERMIONIC
This contrasts with the fermions. The peak spin number for the fermions occurs at spin-2½. Quite what the significance this has, I haven't a clue!
![]()
![]()