Binding Energy Per Nucleon - Large View [POP]

BINDING ENERGY


The mass of a nuclide is not simply the sum of the masses of all the constituent protons and neutrons within the nucleus, because when they are all gathered together inside the nucleus, some of the mass is lost in binding energy according Einsteins famous equation, E=mc2. Thus binding energy represents a negative energy. The Binding Energy per Nucleon (BE/N) is the total binding energy of the nucleus divided by the number of nucleons within the nucleus.

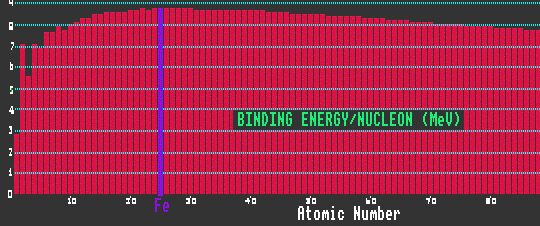
The binding energy per nucleon is small for elements of low atomic number, but for heavier atoms rapidly climbs to a thereafter slowly drooping plateau of 8MeV per nucleon. At 8MeV/nucleon, the binding energy has reached saturation. Nuclides with a high binding energy per nucleon are more stable against radioactive decay than those with less binding energy per nucleon. Iron-56 has the highest binding energy per nucleon, and is thus the most stable element: elements with atomic weight above that of iron, if split into two (as in the case of the fission of uranium) will release energy, as will elements with atomic weight below that of iron if they are made to combine (as in the fusion of hydrogen which occurs within the sun or inside a H-bomb).

Differing nuclides will have differing binding energies, and thus differing baryon (proton plus neutron) number to mass ratios. (Or atomic mass to atomic weight ratios). If the inertial force is dependant upon the number of baryons, and the gravitational force on the atomic mass, then small differences between the inertial mass and the gravitational mass (a fifth force) for different substances would be apparent. Differing substances would fall at differing rates. No such effect has been detected.

See Protons for another possible fifth force.

Shown is a graph of the average isotopic binding energy per nucleon for all the elements from Z=1, hydrogen to Z=102 nobelium. Note the maximum at iron, Z=26.